2021年1月16日上午由伟德国际victor1946国际交流合作处、科研处和伟德国际1946源于英国主办的“科学计算与数据分析（线上）名家讲坛”系列报告第7个报告成功举行。本次报告在腾讯会议举行，由伟德国际1946源于英国尹秀玲主持，伟德国际victor1946科学计算与数据分析团队教师、分数阶微积分领域国内知名专家学者共计60余人参加了本次论坛。伍斯特理工学院张中强副教授做了题为“光滑区域分数阶对流扩散反应方程的高阶方法”的精彩学术报告。

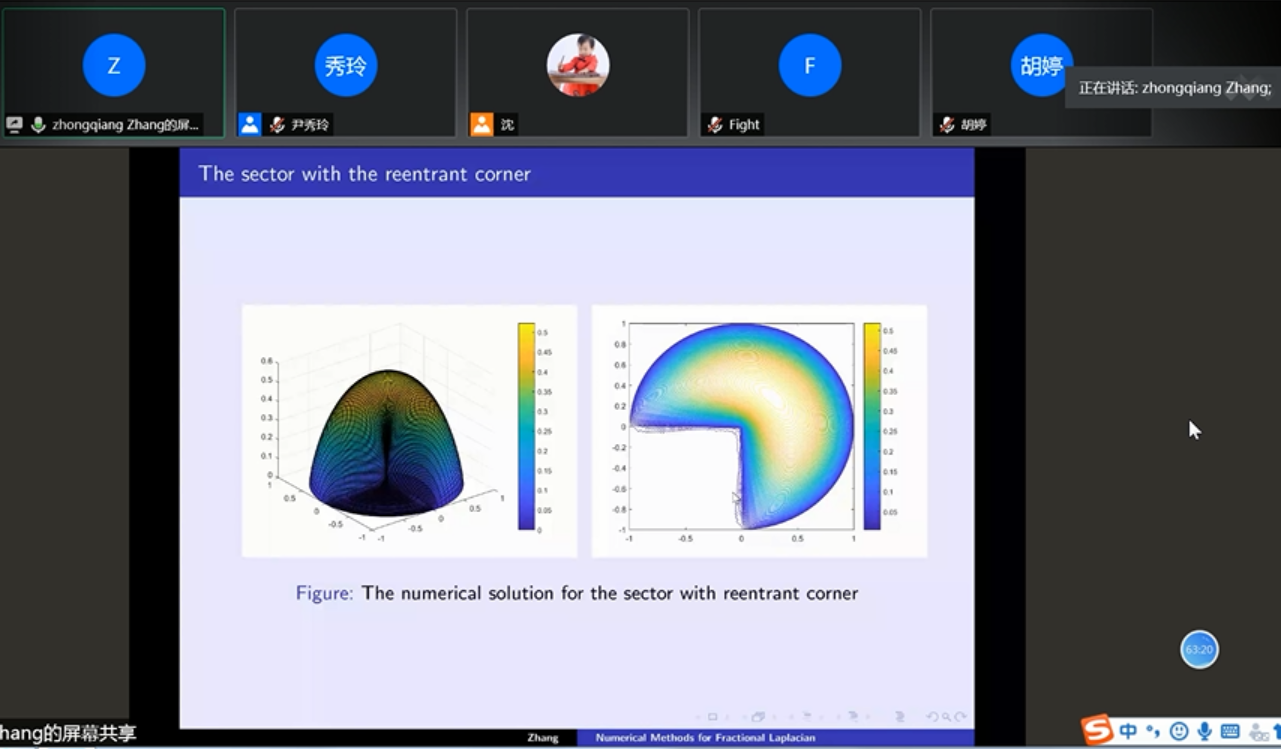
张教授的报告分为两个部分。首先介绍了含有分数阶拉普拉斯算子的偏微分方程的谱方法，借助伪特征函数，解的奇性和傅里叶频率分析，构造了加权的索布列夫函数空间，得出解的正则性和谱方法的最优收敛阶。张教授借助于正交性，分析了谱方法的快速数值实现方法，大大降低了计算量。另外谱方法的精度与解的正则性息息相关，将光滑的右端项不光滑化，比如加入分数阶布朗运动等随机噪声，利用噪声的谱型展开，得到了与噪声指数相关的谱方法的收敛阶。理论分析和数值结果说明了谱方法在随机扰动问题中有很大的优势。 张老师还给大家普及了复杂区域的求解方法：区域扩展和连续延拓。转化后的变系数问题带来了小参数的选取、正则性理论分析、满矩阵的计算和边界振荡现象等新的计算问题。

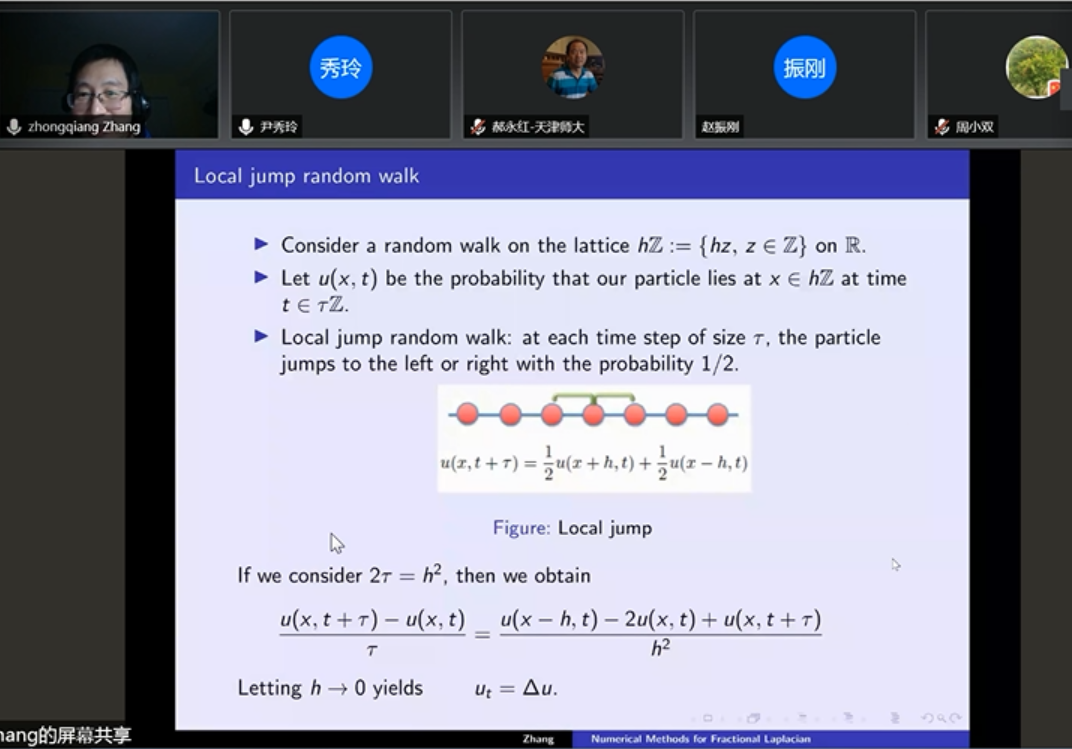
在第二部分，张教授介绍了他与合作者的最新研究成果，高维积分分数阶拉普拉斯算子的分数阶中心差分算子。将生成函数进行傅里叶变换就得到了差分节点上的权。采用高维的快速傅里叶变换、预条件CG方法等进行差分法的数值计算。利用俄罗斯学派通用的区域扩展方法，同样可用差分方法处理复杂区域问题。最后张教授做了总结和展望，谱方法、正则性分析方法与差分法方有望用来求解分数阶NS方程、高维分数阶薛定谔方程、随机对流扩散反应方程和分数阶最优化问题。

报告人简介：张中强，伍斯特理工学院（美国）副教授，博士生导师。张教授，2011年毕业于上海大学计算数学专业。2014年1月获得布朗大学应用数学系博士学位，并获得David Gottlieb 毕业奖。2014年7月起任教于伍斯特理工学院数学科学系。主要研究兴趣计算数学包括积微分方程数值解，计算概率和优化，以及机器学习的计算理论等。在各类著名计算数学期刊发表多篇论文。以第一作者与Professor George Em Karniadakis 合著《Numerical methods for stochastic partial differential equations with white noise》一书。